In the previous post we saw about predicate logic and its formal language. Now we will talk about quantifiers.
UNIVERSAL QUANTIFICATION
Universally quantified propositions are those that speak of a group or set of all or none:
Universal affirmative : All humans are mortal.
Universal negative : No human is mortal .
These propositions have the form of the “if…then” type. So, for example, when we say that “All humans are mortal” we are logically saying, “If something is a human, then it is mortal.” Recalling our previous post on the formalization of subject-predicate propositions, we can now symbolize our universal affirmative in the following way:
∀ x (H x → M x )
Which reads “For all x , if x is a human, then x is mortal.” In the same way, we symbolize our universal negative:
∀x (Hx → ¬Mx)
Which reads “For all x , if x is a human, then x is not mortal.”
EXISTENTIAL QUANTIFICATION
Existentially quantified propositions are those that speak only of some while of a group or set:
Existential affirmative : Some humans are mortal.
Existential Negative : Some humans are not mortal.
These propositions tell us that there is at least one thing that has or lacks the property in question, and they take the form of conjunctions. For example, the proposition “Some dogs are German Shepherds” is not reporting that there is at least one object in the world that is both a dog and black. We can now symbolize our existential affirmation:
∃x (Hx ^ Mx)
Which can be read as “There exists at least one x such that x is a human and x is a mortal.” We now symbolize our existential refusal:
∃x (Hx ^ ¬Mx)
Which reads “There exists at least one x such that x is a human and x is not mortal.”
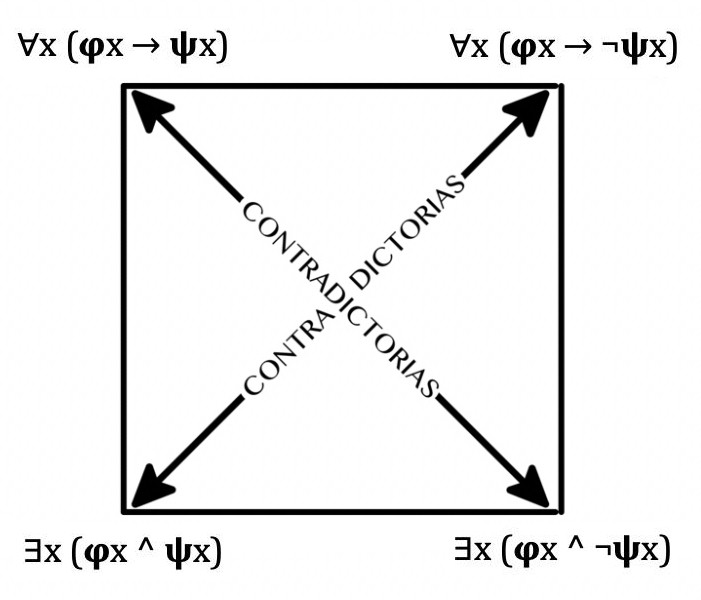
Finally, using the Greek letters 𝛗 and 𝛙 to represent any property symbol, we can represent our general propositions with the following square diagram:
When analyzing this table we can observe two things:
- The propositions [∀x (𝛗x → 𝛙x)] and ∃x [(𝛗x ^ ¬𝛙x)] are contradictory . Thus, from the universal affirmative “For any x , if x is a dog, then x has fleas” and the existential negative “There exists at least one x , such that x is a dog and does not have fleas”, only one of them can be true.
- The propositions [∃x (𝛗x ^ 𝛙x)] and [∀x (𝛗x → ¬𝛙x)] are also contradictory . In other words, of the existential affirmative “There exists at least one x such that x is a dog and x has fleas” and of the universal negative “For any x , if x is a dog, then x does not have fleas” only one can be true, but not both.
Now, what about the contraries relations in our square diagram from our previous post? Shouldn’t the propositions [∀x (𝛗x → 𝛙x)] and [∀x (𝛗x → ¬𝛙x)] be equally contraries where both cannot be true, but both can be false? Not really, and the reason is this: since universally quantified propositions are in the form of conditional statements and if it is the case that the antecedent is false, then no matter the truth value of the consequent, the proposition will be true. Let’s look at an example with both propositions:
- For any x , if x is a square planet, then x has an orbit.
- For any x , if x is a square planet, then x does not have an orbit.
Suppose that the antecedent for both propositions is false; while the consequent of (1) is true but false for (2). Then, according to the truth tables for conditional statements [1] , both propositions are true, so the necessary condition for them to be contrary propositions no longer holds (i.e., they cannot both be true).
In the case of propositions [∃x (𝛗x ^ 𝛙x)] and ∃x [(𝛗x ^ ¬𝛙x)] they cannot be subcontraries either (both can be true but not false), since if “? x” is a propositional function with no true substitution instance, then no matter what “? x ” means, both propositions will be false, and the reason is because existentially quantified propositions have the form of conjunctions , and the truth table for this type of propositions tells us that if the first conjunct is false, then the conjunction in its entirety is false [2] , so the necessary condition to be subcontrary is not met. Let’s see an example with affirmative and negative existential propositions respectively:
- There exists at least one x such that x is a dragon and x is green.
- There exists at least one x such that x is a dragon and x is not green.
Assuming that the first conjunct is false (x is a dragon) for both propositions, false for the second conjunct of (3), and true for (4), then in both cases the propositions are false.
Finally, the implication relation between the subalterns of the diagram from the previous post also does not hold, since we have seen that the propositions [∀x (𝛗x → 𝛙x)] and [∀x (𝛗x → ¬𝛙x)] can be true while the propositions [∃x (𝛗x ^ 𝛙x)] and [∃x [(𝛗x ^ ¬𝛙x)] can be false, so the truth of a universally quantified proposition does not imply the truth of an existentially quantified proposition.
Grades
[1] Truth table for conditionals:
| 𝛗 | 𝛙 | 𝛗 → 𝛙 |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
As you can see, if the substitution instances for ? are false, the entire conditional will be true.
[2] Truth table for conjunctions:
| 𝛗 | 𝛙 | 𝛗 ^ 𝛙 |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Jairo Izquierdo is Director of Social Media and author for the Christian organization Cross Examined . He studies philosophy and theology, with his current focus being classical logic, epistemology, Christian doctrines and linguistics. He is co-founder of Filósofo Cristiano . He is a member of the Christian Apologetics Alliance and a minister of worship at the Christian Baptist church Cristo es la Respuesta in Puebla, Mexico.